
Or: Why soundfield microphones don't come in a wooden ball.
This page is about a DIY project I did to educate myself about soundfield-type microphones, microphone calibration and A-to-B-format conversion. Maybe you can learn a thing or two too.
First, I needed some microphone capsules. I wanted cardioid capsules, but the day I went to the shop, they only had omnis, so I got six of these:
PVM-9745-3P423 (click image for data sheet)
The idea was that I could drill holes in the back of the capsules to convert them into cardioids. That would turn out to be a mistake.
Then, I needed some way of mounting the microphones in a tetrehedral arrangement, so I got a few wooden balls, 19 mm in diameter. Soundfield microphones are usually made to be as open as possible. I though I'd try something different. The closed ball would give all capsules a common cavity, maybe that would help match their directivity patterns? On the other hand, if no sound can reach the back of the membranes, they would have to get an omni characteristic which is not what we want. On the third hand, some sound does enter the ball through the membranes of the other microphones. No further analysis went into this before getting down to the woodwork.
After much frustration, I got four holes in place in about the right directions.

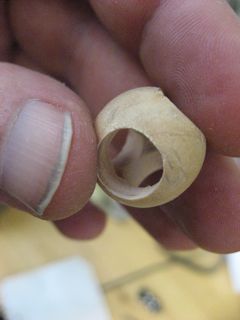
Then I drilled holes in the microphones, hoping to convert omnis to cardioids.

The final assembly:

As one might expect, drilling holes in microphone capsules does nothing to improve their performance. As it turns out, they lost just about all sensitivity below 400 Hz and sounded totally awful. It seemed that I needed capsules that were cardioids to start with. So I made a new wooden ball, picked out the four capsules of a Zoom H2 recorder and put them in there. I don't know which type they are, but they are nominally cardioids and they come with holes drilled in the back from the factory.

The next order of the day was to measure the impulse response of the microphone. For this, I made a signal with unit energy at all frequencies and randomized phase. This signal lasted about a second and a half, was repeated three times and sent out through a loudspeaker at 48 kHz. The sound was recorded with the H2.

To avoid reflections, it was necessary to place the loudspeaker and microphone far enough away from walls and the floor that a useful impulse response could be picked up before the first reflection. I went for a minimum path length for the reflections which was 1m longer than for the direct sound, giving me a usable impulse response of 1/340s.
The plan was to shift the phase of the recorded signal back with the same magnitude as in the excitation signal, but in the opposite direction. Before that could be done, the sampling frequencies had to be matched, since the recording device and the playback device were not synchronized. Measuring the autocorrelation function of the recorded signals, it seemed that if the playback device was running at exactly 48 kHz, then the recording device was running at 48000.99 +- 0.01 Hz. This may not seem like a big discrepancy, but uncorrected, it will totally ruin the high frequency parts of the impulse response. To resample the signal, it was first oversampled at 16x, then interpolated with cubic interpolation. Finally, to correct for the frequency characteristics of the loudspeaker, the impulse response was measured with a presumably better microphone (Hansen CRI-87):

The impulse response of the soundfield-type microphone was measured four times, once with each capsule facing the loudspeaker. Each recording had four channels, giving a total of sixteen measurements: Four with capsules facing the loudspeaker and twelve with capsules at 109° angle from the loudspeaker. The average spectrum of these two types of impulse responses:
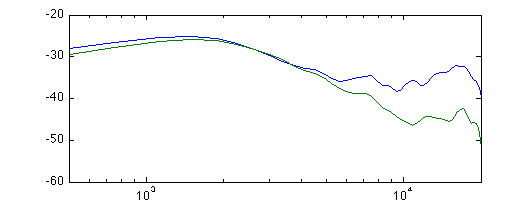
An ideal cardioid would have a 9.44 dB difference in response head on compared to 109° angle. In this case, the difference is just a couple of dB at low frequencies and only reaches this level around 10 kHz. Around 3 kHz there is no difference. Clearly not very useful. The phase response:
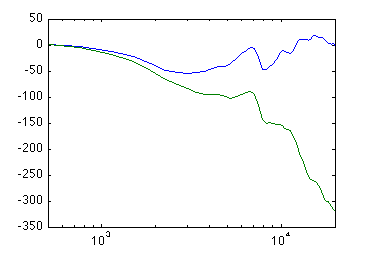
The backwards-pointing capsules are phase shifted with about 320 degrees compared to the forwards-pointing capsule at 20 kHz. This corresponds to an extra travel length of 15 mm. This makes good sense, since the back capsules are actually 12.7 mm further away from the loudspeakers and the remaining 2.3 mm can easily be brushed off as diffraction effects and the membrane being a couple of millimeters inside the surface of the ball.
Next attempt: Drill holes in the ball to allow more sound to reach the inside, and hence the back side of the membranes. This is the mechanism which makes cardioids cardioids.

Unfortunately, there is not enough room to drill the holes at the positions half-way between two capsules and of the four locations that are equally far from three capsules, one is already occupied by the leads coming out. Even so, this is where the holes go. As you see, hot glue was added at some point to be sure that no sound leaked in outside the membranes. This might also help explain the extra 2.3 mm travel length.
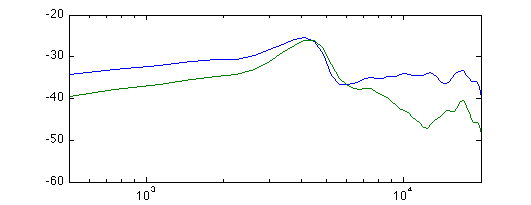
The extra holes seem to have the desired effect at low frequencies, giving about 5 dB difference between head-on and backwards-pointing capsules. This corresponds to a useful subcardioid characteristic. However, there are problems around 4-5 kHz, where the backwards-pointing capsules actually pick up more sound than the forwards-pointing one. The phase response:
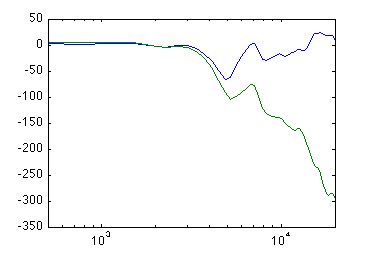
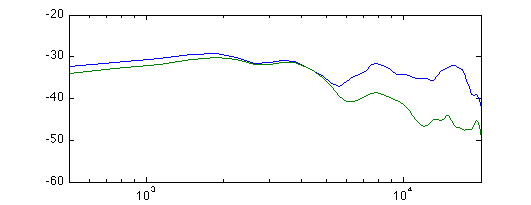
Could the peak around 4-5 kHz be a helmholtz resonance perhaps? The holes are about 3mm deep, 4mm in cross section, there are three of them, and the internal volume of the ball is something like a ball with r=6.5mm. That would give a helmholtz resonance at 5.7 kHz. About the right ballpark. If we could move it to about 12 kHz, it wouldn't do so much harm, maybe even some good. How can we do that? We could increase the area of the holes by a factor of 7, but there is no room for that. Alternatively, we could reduce the inner volume by the same factor. Ok, so I fill the microphone with sand. Magic sand, since that is what happens to be available:

Hopefully, it won't make its way to the membranes. Small dabs of cotton prevent the sand from falling out of the holes. Result:
Phase:
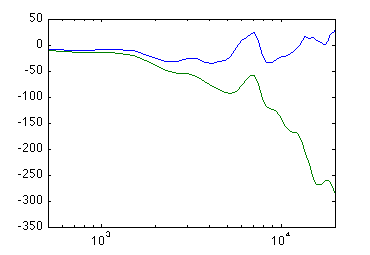
This didn't work, and seems to bring us back to the closed ball situation. It seems that the wooden ball, although practical for holding the capsules, is not a good solution. So, after another good deal of frustration

I got the capsules into a more conventional, open arrangement:

The resulting amplitude and phase response:
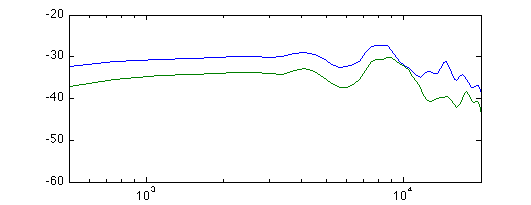
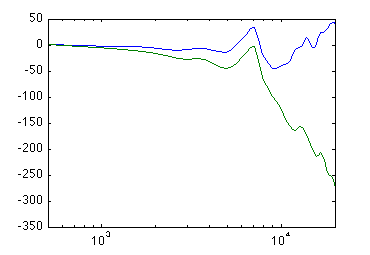
At least now, it seems that the helmholtz resonance is gone, and up to 9 kHz, the ratio between front and back gain is nice and constant. However, the two curves kiss at 10 kHz. What could the reason be? Out of ideas, I plug a small dab of cotton inside the mike:

Result:
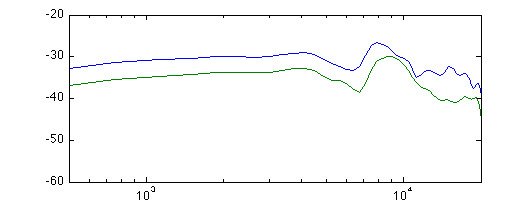
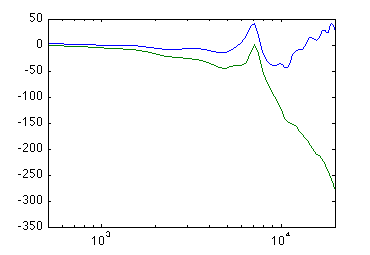
It didn't change much but I like what it did change, so I put more cotton in:
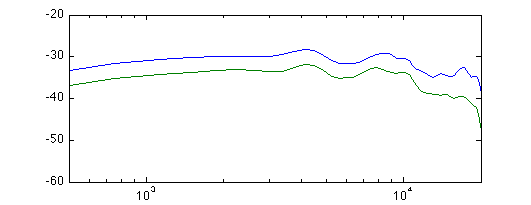
Success! Maybe there was a resonance of some sort in the cavity resonance between microphones, and the cotton dampened it. In that case, I should have tried cotton inside the wooden ball instead of sand, but that's a bit late now.
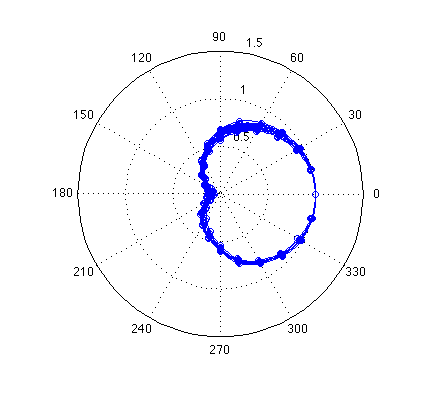
Next, I wanted to look at the full polar diagram and measured the impulse response of one of the capsules in 24 directions in a plane containing its front direction. Up to 7.5 kHz the amplitude response (even on a linear amplitude scale as below) looks hunky-dory. This is 18 curves plotted on top of each other:
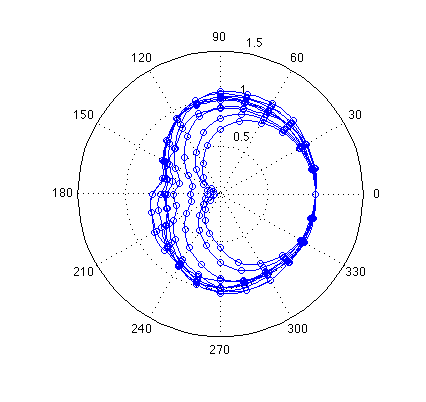
However, from 7.5 kHz up to 10.875 kHz something unfunny happens:
From 10.875 kHz to 20.25 kHz things settle down and we start to see beaming:
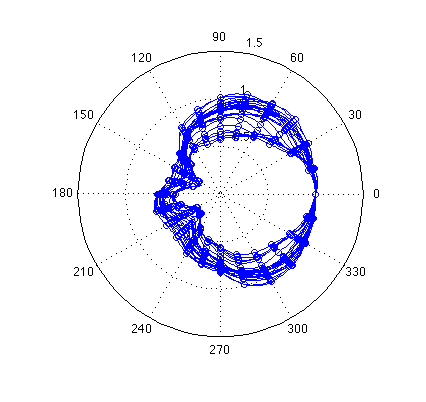
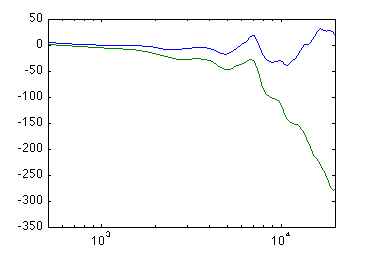
The main problem with this microphone is between 7.5 and 11 kHz. Anyway, this arrangement seems to give a much cleaner directivity patterns than the original setup of the H2, which I also measured. Renormalizing the last measurements against a better reference microphone (Neumann KM140) shows a clear resonance around 9 kHz:
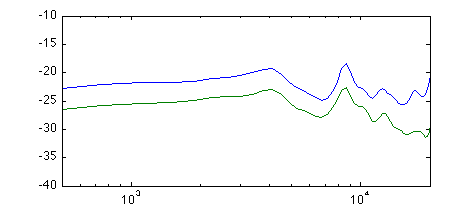
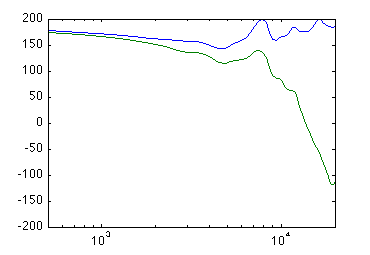
(the phase is evidently flipped 180°).
The front-to-back phase difference, plotted on a linear frequency axis:
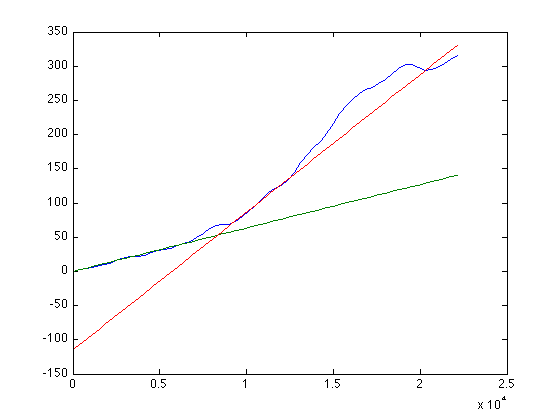
The red and green lines correspond to group delays equal to 6 mm and 19 mm, respectively. When we plot the front-to-back gain difference capsule by capsule, the picture looks less rosy:
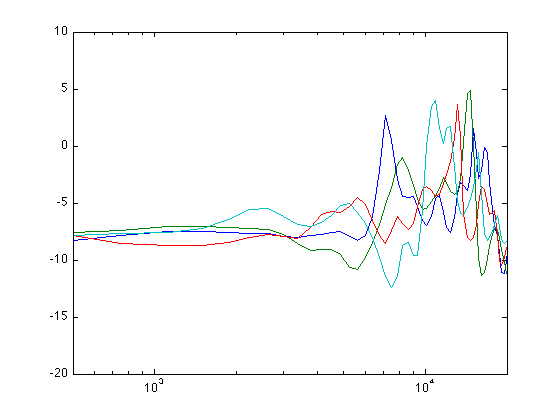
The various resonance peaks don't overlap. Maybe it is an accident, or maybe is is because they are coupled resonators. Either way, we need to do something the peaks crossing (or even approaching) 0dB. The strange thing is that this did not show up in the polar plot... Maybe there is a lack of rotation symmetry... Ouch. Maybe it has something to do with the fact that the front-back curves were measured with the microphone hand-held, while the directivity plot was measured on a tripod.